1.偏差値って何だろう?
実際に高校を選ぶ場合、入学試験がある以上、やはり「学力」が大きなポイントになってきます。
「学力」を表す数値として「偏差値」がよく使われます。この偏差値とは一体何物なのか、意外に誤解されている面があるため、改めてよく理解しておきたいものです。
偏差値の説明には、数学の「統計学」の知識が必要になります。ここでは複雑な算出過程は省略して、まず偏差値を使うとどういった利点があるかを説明するために、A君に登場してもらいましょう。
A君は7月にX公開模試(500点満点)を受けました。この試験の結果を得点分布で表すと図-1のようになり、平均点は320点、A君の得点は380点で、受験者1万5000人中3,000番の順位で、偏差値は60でした。
ところが、同じA君が受けた9月のX公開模試は受験者数が増えて1万8000人となり(ただし増加した受験生の学力の偏りはなかったものとします)、A君は3,500番となってしまいました。平均点340点、得点は400点、偏差値は前回と同じ60でした。
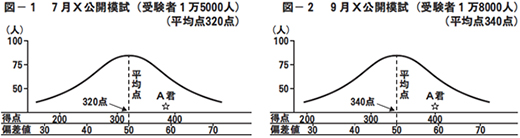
さて、A君だけに注目して、7月と9月の成績を単純に比べてみると、得点は20点増えたものの、順位は500番も下がってしまいました。平均点が上がり、受験者が増えたのだから当然といえば当然です。しかし、A君は「自分の学力は、いったいどれくらいなのだろう。毎回毎回、受験者数や平均点を見て考えなければならないのかな?」と考えるに違いありません。ここに偏差値の存在価値があります。偏差値だけは前回と同じ60だったことから、A君の位置は7月と9月でほぼ同じであると理論的に説明することができます。ただし条件として、受験者数は多少変化しても、受験者の学力層および試験問題の質が変わらないことが必要です。

上の図のような得点分布が得られると、平均点を核とした特殊な計算を行い、標準偏差という統計学的な「ものさし」になるものを導くことができます。それをさらに操作して、もっと感覚的にわかりやすいように、平均点にあたる位置を50として、ほぼ全員の数値が25~75くらいの幅に入るようにしたものが偏差値です。こうして得られた偏差値は、「全体から見た個々の学力の位置」を表現したもので、試験ごとに全体のでき具合が変わっても(平均点や順位のつき方が変化しても)、受験者のグループ(母集団と呼びます)が同じであれば、偏差値の数値をもとに、およその自分の学力の位置を知ることができるのです。
しかし、ここで注意しなければならないのは、さまざまな意味で「偏差値は万能だろうか?」ということです。また、前述のような条件がそろったときには有効に使えますが、最近は各種の公開模試があり、条件が変わったり、意識的に条件を変えて模試が行われることもあります。そのときは学力が変わらなくても偏差値がそれぞれ変わってきますから、条件によって使い分けしなければなりません。次に、条件が変わることで偏差値も変わることについて説明します。
2.偏差値は万能だろうか?
以下のような場合、偏差値も変わってきます。Bさんに登場してもらい、具体的に見ていきましょう。
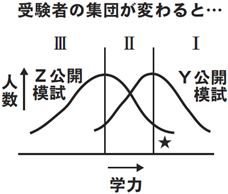
Bさんは10月にY公開模試を受けました。その結果を得点分布図で表すと図-3のようになります。300点満点で平均点は210点でしたので、ここが偏差値50ということになります。Bさんの得点は230点で、偏差値は54と出てきました。
Y公開模試の受験者は学力をⅠ~Ⅲの3段階に分けた場合、比較的上位のⅠとⅡの層が中心で、Bさんの成績は図-3の★の位置でした。
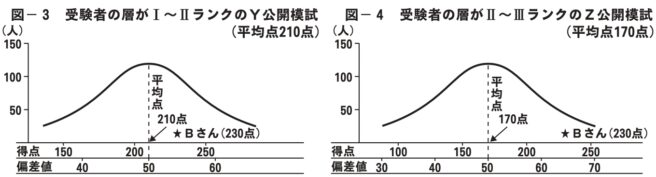
ところで、同じ10月に、Bさんが受験者の層がⅡとⅢのランクを中心に構成されたZ公開模試を受けていたとします。そして、問題のレベルがY模試と同じで、Bさんのコンディションも変わらなかったとすると、ほぼ同じ点がとれるはずです。ところが、受験者全体のレベルが下がっているため、平均点は170点と40点も下がり、この試験では170点が偏差値50となります。したがってBさんの偏差値はグンと上昇します(図-4)。
Bさんの偏差値は66。偏差値について詳しくなかったBさんは、「でき具合は同じだったのに、いったいどちらを信じたらいいの?」と悩んでしまうことでしょう。偏差値としてはどちらも正しいのですが、受験者全体のレベルが変わるためにこのような現象が起こってくるのです。つまり、受験者本人の学力が変わらなくても他の条件が変わると、「ものさし」が動いて、数字は上がったり下がったりしてしまうのです。

実際には、模試によっては問題のレベルがかなり高いこともあります。たとえば、公立高校と私立高校では一般に入試問題の質やレベルが異なることが多く、より正確な判定をするためには、問題のレベルを変えた模試が必要となってくるのです。このようなことを述べてくると、「偏差値は信用できない」と思う人も出てくるでしょう。しかし、それは誤った考えです。ひとりの受験生が受ける模擬試験は2種類か3種類です。また、それぞれの模試で、回ごとに受験生のレベルや問題の質はそれほど変わるものではありません。したがって、自分が受験して得た偏差値がどんな性格のものであるかをしっかり認識して、使い分ければよいわけです。そして、それはそんなに難しいことではないのです。
3.偏差値は動く
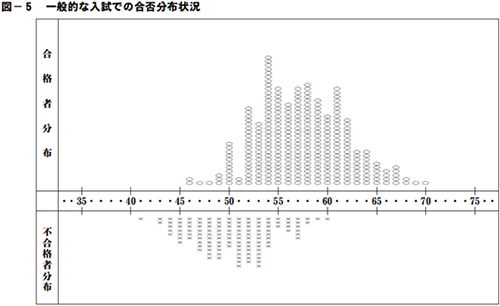
前述のように、「偏差値」について正しく理解していれば、志望校の合格可能性を知る上で非常に有用です。しかし、一方で「実際の入試では必ずしも偏差値どおりに合否が決まらない」ということも起きてきます。上図は「一般的な入試での合否分布状況」です。合格者と不合格者がある程度の幅で重なっています。つまり、同じ偏差値でも、合格する生徒がいる一方で不合格の生徒もいるわけです。
これはどの高校で調べてもごく普通におこる現象で、以下のような理由が考えられます。
a) 私立高校の入試問題の特殊性
私立高校の入試は各校独自の問題を使って行われます。つまり、私立高校の問題のスタイル・内容・難易度は私立高校の数だけあるわけです。どんなに工夫しても、1種類の模擬試験ですべてのタイプの入試問題をカバーすることは不可能です。たとえば、国際基督教大学高校などはユニークな出題をすることで知られており、標準的な模擬試験の偏差値では合否判定を正確に予測しえなくなっています。
b)私立高校の選抜方法・合否基準の多様さ

多くの私立高校では、筆記による学力試験に加えて、面接試験や作文・その他によって、ペーパーテストでははかれない資質(性格や考え方)を合否の基準に入れています。さらに、調査書(内申書)の扱いや、一般入試における、第一志望・第二志望者への優遇制度などがからむと、合否の分かれめは相当に複雑なものになります。以上のようなことが、合否を複雑にしている理由です。
c)偏差値に表れない受験生の性格
一人ひとりの受験生の偏差値は試験ごとに変動します。そこで一般的には、何回かの平均をとって使います。それでも実際の入試では、学力以外の要素がどうしてもかかわってきます。日ごろの実力を十分に発揮できるかどうか、どたん場で結果を左右するのが受験生の「性格」です。開き直って普通以上の力を出す人もいれば、あがってしまって半分の力も出せないという人もいます。
このような受験生の性格や当日のコンディション(体調など)が、偏差値どおりにならない最大の原因といえます。一般的にこうした原因で、偏差値は3~4上下するといわれています。




